动态规划|力扣62.不同路径、力扣63.不同路径||

1.力扣62

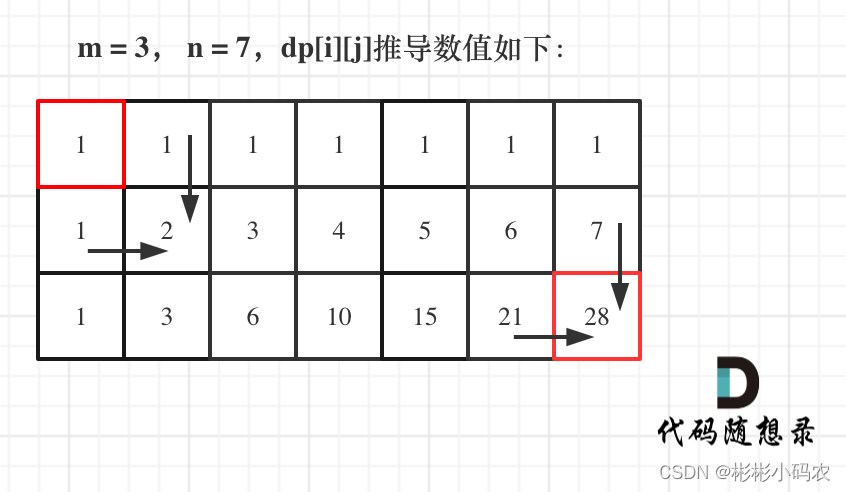
         本题和昨天的斐波那契数的递推公式很类似，不过是在一维的基础上升级为二维，首先我们设到达（i，j）的路径有dp[i][j]种，而能到达（i，j）处的只有（i-1，j）和（i,j-1），所以dp[i][j]=dp[i-1][j]+dp[i][j-1]，至此推出递推公式，接下来确定遍历顺序，从左至右，从上至下。

public int uniquePaths(int m, int n) {//确定dp数组int[][] dp = new int[m+1][n+1];//初始化边界for(int i=0;i<=m;i++){dp[i][0]=1;}for(int i=0;i<=n;i++){dp[0][i]=1;}//确定遍历顺序for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m-1][n-1];}

2.力扣63

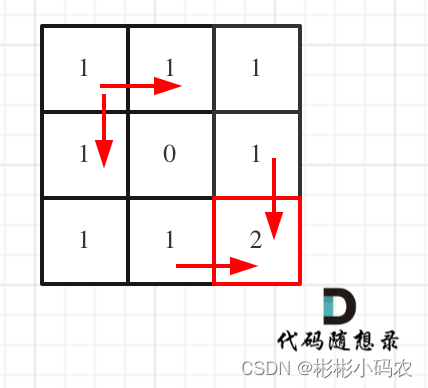
        本题在上一题的基础上加上了障碍物，而我们需要设置一个dp的二维数组，用来存储结果，而obs二维数组用来遍历障碍物的位置， 而递推公式和遍历顺序不变。

public int uniquePathsWithObstacles(int[][] obstacleGrid) {//定义m*m的地图int m = obstacleGrid.length;int n = obstacleGrid[0].length;//定义dp数组int[][] dp = new int[m][n];//若出发点和重点有障碍物，则停止if(obstacleGrid[m-1][n-1]==1||obstacleGrid[0][0]==1){return 0;}//初始化-》这里边界上若有障碍物，我们应把障碍物及其之后的位置填为0for(int i=0;i